Georg Cantor

The main focus of this paper is to describe the development of Georg Cantor as a mathematician and to highlight that he indeed reached profound visions in this field. The birth of Cantor took place on 3 rd of March, 1845 in St. Petersburg, Russia and hence the foundation of this prodigious mathematician can be said to be as fascinating as the mathematics that he later created. His extensive mathematical fluency was evident at the beginning and led him through pathways of the University of Berlin and the University of Göttingen.

In essence, Cantor’s significant work was in the field of set theory in which he named an extraordinary cardinality known as transfinite numbers. He went into the depths of transfinite numbers, to tell us about the sizes and characteristics of sets. The foundation for a rich structure from which it became possible to understand the mysterious about the infinite was laid down by Georg Cantor when he defined a “set” as a collection of distinct elements. He proved to the learned audience that not all infinities are equal in size.

The set of natural numbers was found to be infinitely greater than the set of positive integers and every member of the new set corresponded in a beautiful way to some natural number. Still, it was the real numbers that was having a peek into the real supply the most surprising type of infinity that was in fact a lot worse than the natural numbers in the sense of the eminent cardinality they had in common.

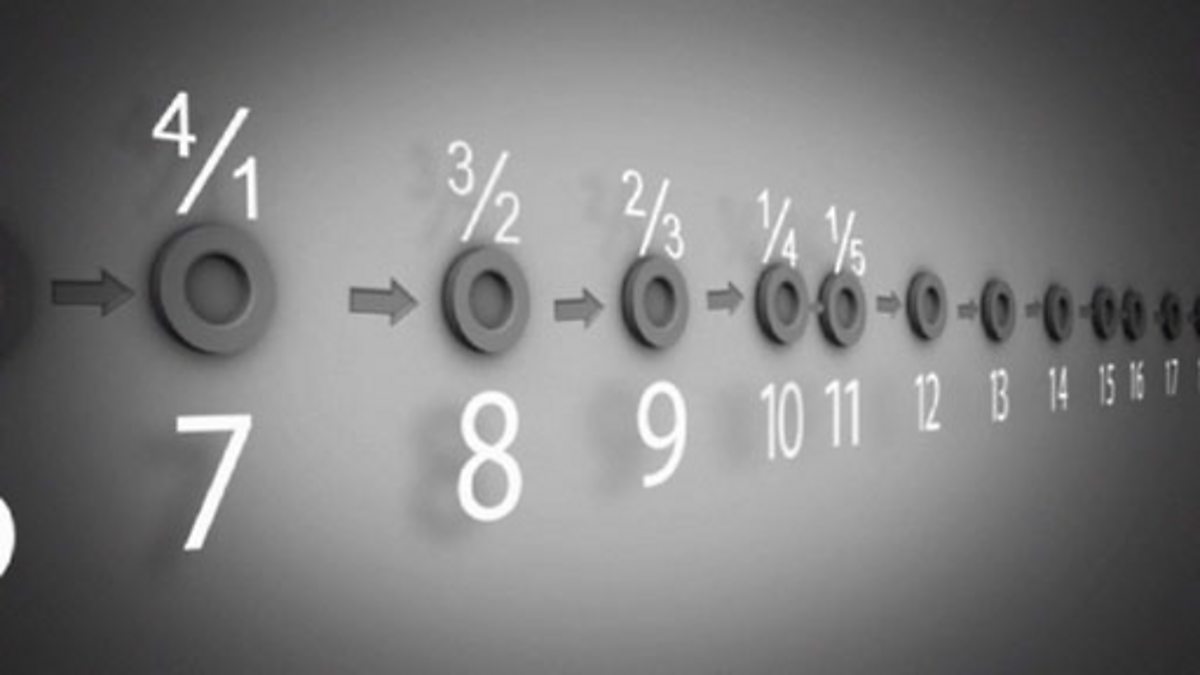
Among Cantor’s her outstanding and ambiguous statements was the continuum hypothesis which being a conjecture described the middle ground between the set of natural numbers and the set of real numbers. Science thus still finds itself in the dark about the answer to that question, within the contexts of traditional set theory; yet this very hypothesis suggested a type of independence.

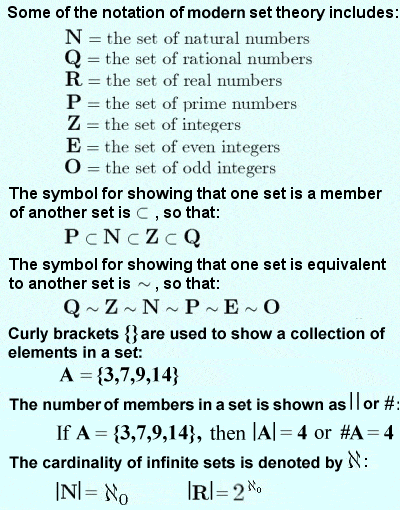
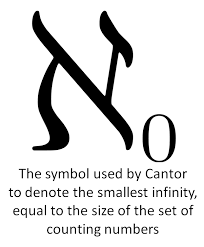
After careful scrutiny and denial, however, all entailed or attaching to Cantor’s contributions started to receive public praise. The victories from his academic achievements include his professorship of the University of Halle and recognition from superior societies. However, his personal life was on the opposite side of such success and failures and included depression and other mental issues in spite of the criticism.

Georg Cantor's legacy in mathematics is a testament to his fearless exploration of the infinite. His work forever altered our comprehension of the mathematical universe, inspiring generations of thinkers to embark on their own quests through the boundless landscapes of knowledge. Cantor's spirit of inquiry continues to resonate, a beacon for those who dare to navigate the infinite.